Applications of Genetic Algorithms in Chemistry
Click here to return to my home page
Background: Genetic Algorithms

The genetic algorithm is a search technique based on the principles
of natural evolution. It uses operators that are analogues of the
evolutionary processes of mating (or ``crossover'' at the gene level),
mutation and natural selection to explore multi-dimensional parameter
spaces. The GA belongs to the class of evolutionary algorithms, which
also includes evolution strategies, differential evolution and genetic
programming.
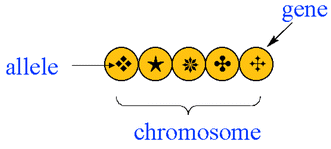
In principal, a GA can be applied to any problem where the variables
to be optimised (``genes'') can be encoded to form a string
(``chromosome'') - as sheown below. Each string represents a trial
solution of the problem. By analogy with biology, the values of the
individual variables are known as ``alleles''.
In a typical GA, a population of individuals evolves for a
certain number of generations - which is either fixed in
advance or may depend on some convergence criterion.
The initial population corresponds to the starting set of
individuals which are to be evolved by the GA. These individuals are
usually generated randomly, though it may sometimes be beneficial to
use any available prior knowledge or chemical intuition in the
generation of the initial population (taking care not to bias the
search too much).
Fitness is an important concept for the operation of the GA.
The fitness of a string is a measure of the quality of the trial
solution represented by the string with respect to the function being
optimised. Thus, high fitness corresponds to a high value (in a
maximisation problem) or a low value (in a minimisation problem) of
the function. If the upper and lower limits of the function being
optimised are known, then absolute fitness may be used -- where
fitness values may be compared from generation to generation.
Otherwise (as in most GA applications), dynamic fitness scaling
can be adopted, where, in each generation the fitnesses of all the
individuals are scaled relative to the best and worst members of the
current population. Fitness is important in determining the
likelihood of an individual taking part in crossover and also in
deciding which individuals will survive into the next generation.
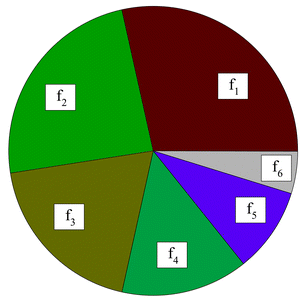
Selection refers to the way in which individual members of the
population are chosen for subsequent crossover. There are a number of
selection methods, the two most common being ``roulette wheel'' and
``tournament'' selection. In roulette wheel selection (shown
below), a string is chosen at random and selected for crossover if its
fitness value (f_i) is greater than a randomly generated number
between 0 and 1, otherwise another string is chosen and tested. The
analogy with a roulette wheel is apparent if one envisages a roulette
wheel with a slot for each member of the population, where each slot
has a width (and therefore a probability of the ``ball'' dropping into
it) which is proportional to the fitness of the corresponding member
of the population. Tournament selection involves picking a
number of strings at random from the population to form a
``tournament'' pool. The two strings of highest fitness are then
selected as parents from this tournament pool.
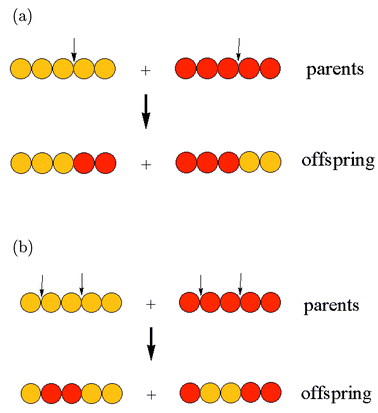
Crossover is the way in which ``genetic'' information from two
(or sometimes more than two) ``parent'' strings is combined to
generate ``offspring''. In one-point crossover (a below),
two parent strings are cut at the same point and offspring are formed
by combining complementary genes from the parents (i.e. the first part
of parent 1 with the second part of parent 2 and vice versa).
In two-point crossover (b below), the two parents are cut at
two points and offspring are formed by inserting a the central
sequence from parent 1 into parent 2 and vice versa. Other types of
crossover are possible, such as uniform crossover, where
offspring are generated by taking a certain number of genes from each
parent, with no restriction on where these genes occur in the
string.
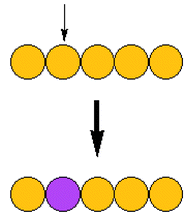
Mutation - While the crossover operation leads to a mixing of
genetic material in the offspring, no new genetic material is
introduced, which can lead to lack of population diversity and
eventually ``stagnation'' - where the population converges on the
same, non-optimal solution. The GA mutation operator helps to increase
population diversity by introducing new genetic material. This can be
accomplished by making a random change to one or more randomly chosen
genes in an individual (as shown below). In static mutation,
the mutated gene is assigned a completely random value, while in
dynamic mutation its value is changed by a small, random amount
about its original value.
``Natural'' selection - In biological evolution the concept of
the ``survival of the fittest'' (or best adapted to the environment)
is a strong evolutionary driving force. In the case of a GA, although
the selection is clearly not ``natural'', individuals (be they
parents, offspring or mutants) are likewise selected to survive into
the next generation on the basis of their fitness (their quality with
regards to the quantity being optimised). There are many
modifications of the selection step, however: for example all mutants
may be accepted, none of the parents may be accepted, or only the best
parents may survive (the so-called ``elitist'' strategy - adopted so
that the best member of the population cannot get worse from one
generation to the next).
Schemata - The GA operators essentially exchange information
between individual strings to evolve new and better solutions to the
problem being optimised. A critical feature of the GA approach is
that it operates effectively in a parallel manner, such that many
different regions of parameter space are investigated simultaneously.
Furthermore, information concerning different regions of parameter
space is passed actively between the individual strings by the
crossover procedure, thereby disseminating genetic information
throughout the population. The GA is an intelligent search mechanism
that is able to learn which regions of the search space represent good
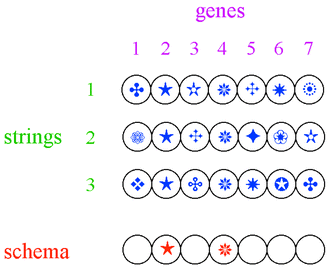
solutions, via the recognition of schemata. The figure below shows
three strings of seven variables (genes). The values of the variables
(alleles--represented by blue symbols) are such that the three strings
have identical values for genes 2 and 4. These three strings,
therefore, contain a common ``schema'' (or building block, shown in
red at the bottom of the figure) corresponding (in this example) to a
star at position 2 and a snow flake at position 4. In a real
application of a GA, a good schema (corresponding to a set of optimal
or near-optimal variables) may be implicitly recognised and propagated
within the population, if it leads to individuals of relatively high
fitness.
Applications






